共计 5473 个字符,预计需要花费 14 分钟才能阅读完成。
任何能够证明流体数学在何处失效的人,将获得 100 万美元的奖金。如今,通过专门训练的人工智能系统,研究人员在这个问题的简化版本中发现了大量新的候选案例。

Samuel Velasco / _Quanta Magazine_
引言:流体方程的世纪难题
大约 200 年前,物理学家克劳德 - 路易·纳维和乔治·加布里埃尔·斯托克斯完成了一组描述流体如何旋转的方程。近两个世纪以来,纳维 - 斯托克斯方程一直被视为描述现实世界流体行为的无可置疑的理论——从穿行于大陆之间的洋流,到包裹飞机机翼的空气。
然而,许多数学家怀疑这些方程深处隐藏着缺陷。他们预感,在某些情况下,该理论会失效。此时,方程将预测流体以某种非物理的、难以理解的方式运动——例如,旋转成不可能的高速涡流,或瞬间逆转流动方向。正如数学家所说,方程中的某些量将变得无限大,或者说“爆炸”。
尽管付出了巨大努力,至今尚未有人能提出纳维 - 斯托克斯方程失效的具体情况。做到这一点——或者反过来,证明方程永远不会爆炸——即可赢得 100 万美元的奖金。因此,作为解决纳维 - 斯托克斯问题的前奏,数学家们在一系列简化的流体方程中寻找爆炸(也称为奇点),例如那些只在一维空间中成立的方程。
他们确实找到了这些奇点。但基本上,所有已发现的奇点都是“稳定的”,意味着它们可以以多种可能的方式形成。在最现实的流体理论中,包括纳维 - 斯托克斯方程,爆炸(如果存在的话)很可能要微妙得多,必须以难以想象的精确方式发生。这些“不稳定的”爆炸几乎不可能被发现,犹如大海捞针。
在这些现实的理论中,“许多人认为存在奇点,但它们是不稳定的,因此我们从未见过它们,”普林斯顿大学数学家查理·费弗曼说,正是他制定了百万美元的纳维 - 斯托克斯难题。
人工智能如何助力奇点搜寻
如今,一组数学家开发了一种训练机器识别这些幽灵般缺陷的方法。在 9 月发布的一篇预印本论文中,他们重新审视了已知存在稳定奇点的简化流体方程,并在其中发现了额外的潜在爆炸情景——包括不稳定的情景。这是首次在多于一维的流体中发现可能的不稳定奇点。
该团队还在其他几个流体方程中找到了各种不稳定的奇点候选。他们尚未发现任何价值百万美元的奇点,也仍需严格证明他们所发现的那些确实会导致爆炸。但他们在简单模型中成功找到潜在不稳定奇点,这提高了在高风险场景中发现不稳定爆炸的希望。
“不稳定奇点的想法不再阻碍奇点的发现,”未参与这项新研究的费弗曼表示。
奇点搜寻的技术挑战
纳维 - 斯托克斯方程的解捕捉了流体运动的瞬间永恒。求解流体某个初始状态的方程,就能告诉你流体在空间每个点、每个时刻的速度。在简单的解中,流体可能始于平静并永远保持平静;在更复杂的设定中,温和的洋流可能会合并成漩涡和涡流。最大的谜团在于:每一个解——每一个满足纳维 - 斯托克斯方程的可能流体历史——是否在任何地方、任何时刻都有意义。
但处理三维流体的纳维 - 斯托克斯方程极其困难,因此数学家们从更易处理的版本入手。例如,欧拉方程假设流体流动时没有内部摩擦或粘度。在这些无摩擦的流体中,能量不会耗散,因此它们应该比粘性流体更容易爆炸。
然而,即使在这种更简单的情况下,找到爆炸解也异常困难。流体方程通常复杂到无法直接用纸笔求解。因此,一种常见的方法是使用计算机模拟流体运动,并大致了解似乎会产生爆炸的条件。如果能精确识别出导致爆炸的条件,或许就能利用这些知识严格证明爆炸确实存在。
这正是托马斯·侯和罗国在 2013 年采用的方法。他们模拟了一个罐子中的数字液体,让液体的上半部分朝一个方向旋转,下半部分朝相反方向旋转,然后使用欧拉方程让系统随时间演化。最终,在相反流动沿罐子边界相遇的点,涡度(衡量液体围绕某一点旋转程度的量)变得极大——大到计算机无法处理。
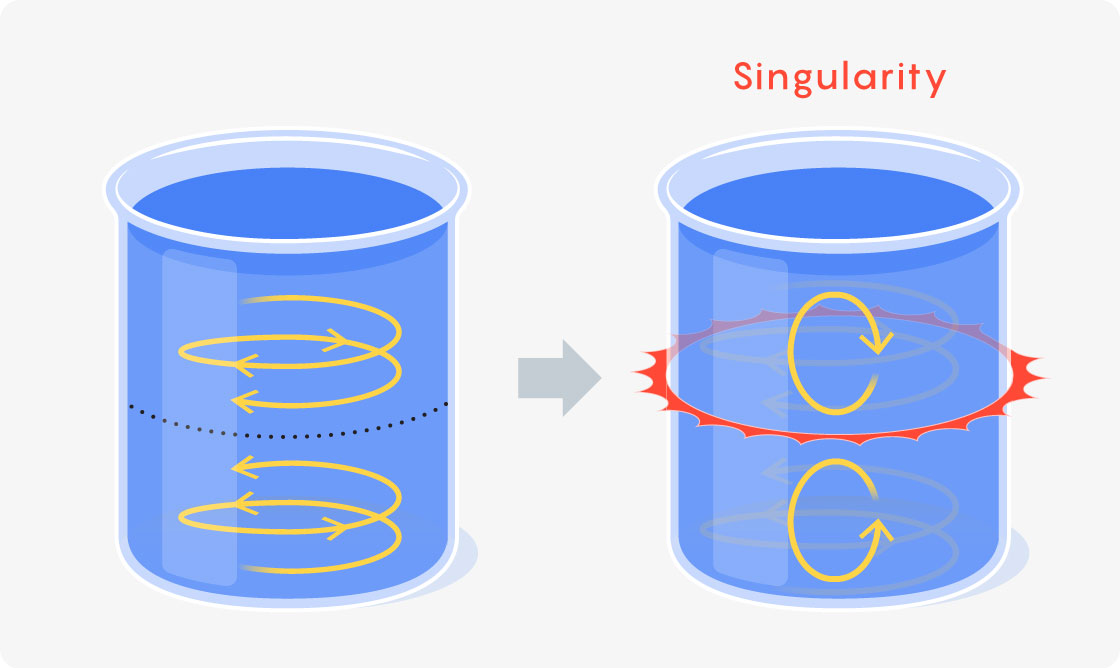
Mark Belan / _Quanta Magazine_
这暗示类似的条件可能导致爆炸,但并不能保证。“3D 欧拉方程的所谓奇异解遍布墓地,”费弗曼说。
侯与另一位合作者陈嘉杰花了近十年时间才去掉了“所谓”这个词。2022 年,他们利用计算机证明了奇点候选暗示了真正奇点的存在。这是一个里程碑式的证明,让数学家们渴望将前沿推得更远。
这项研究依赖于计算机模拟,意味着对数字流体初始状态的微小调整(或任何数字舍入误差)不会影响流体的命运。即使情况略有不同,奇点仍会在罐子边界发生。
因此,这个奇点是稳定的。但奇点未必稳定。爆炸可能只有在流体以最微妙的方式设置时才会发生。在这种情况下,对初始排列的任何微小调整都会阻止流体爆炸。
许多数学家推测,如果奇点确实潜伏在更现实的流体方程中,它们将像这样不稳定,毫无预警地突然出现。
它们也将更难被发现。
物理信息神经网络的应用突破
通过计算机模拟追踪不稳定的奇点候选几乎不可能。首先,你需要极其幸运地恰好落在流体正确的初始配置上——这就像试图将一支笔完美地平衡在笔尖上,纽约大学数学家特里斯坦·巴克马斯特说。然后,为了保持平衡,还必须完美地将流体从一个时刻演化到下一个时刻,因为即使是最小的偏差也会使其偏离不会爆炸的路径。
计算机无法实现无限精度。它们不可避免地会引入数值误差,这些误差虽然微小,但会阻止不稳定奇点的形成。“这就像风吹在你的笔上,”巴克马斯特说。


根据托马斯·侯(左)和陈嘉杰在 2022 年的里程碑式证明,围绕圆柱体旋转的无摩擦流体可以“爆炸”。
Vicki Chiu; Courtesy of Jiajie Chen
因此,几乎所有的爆炸候选都是稳定的。
于是,巴克马斯特和他的同事们开始研究一种可能“防风”的方法来寻找不稳定的奇点。
他们并非一开始就打算这样做。2021 年,他们使用神经网络作为一种新方法,不加区别地搜索任何类型的奇点候选。一般来说,神经网络是由大量数字定义的函数。这些数字通过高效的“训练”过程进行仔细调整,包括猜测、检查和改进,直到函数能够执行某些期望的任务。例如,如果你使用数千张标记过的猫和狗的照片来校准神经网络,它就会“学会”接收从未见过的未标记图像,并将其分类为“猫”或“狗”。
巴克马斯特团队转向了所谓的物理信息神经网络(PINN)。与图像分类神经网络不同,PINN 不是通过研究外部数据来学习。相反,它采用一个偏微分方程——描述系统如何随时间变化的方程——并调整自身,直到能够表示解决该方程的函数。例如,它可以采用流体方程,并训练自己逼近一个捕捉流体有效历史的函数,这个历史可能包含一个奇点。
没有时间,所以你不在乎它是否不稳定。
特里斯坦·巴克马斯特,纽约大学
然而,没有计算机技术可以直接呈现奇点的无限性。想象一下播放流体模拟并观察其随时间向前移动。你可能将某个量(例如流体中不同点的速度)表示为图表上的曲线。随着流体变化,曲线也会变化,就像电影一样。如果曲线从一帧到下一帧变得陡峭得多,流体可能正在接近奇点。但模拟无法到达最终目的地:在曲线变得无限陡峭之前,计算机将耗尽内存,导致程序崩溃。于是你无法确切知道将会发生什么——是否真的走向了爆炸。
为了避开无限性的不便,数学家们最近将搜索重点放在具有一种特殊性质(称为自相似性)的奇点上。这意味着有一种方法可以拉伸一帧中的速度曲线,以匹配后一帧中更陡峭的速度曲线。因此,要捕捉潜在的奇点,你不再需要试图观察曲线变得无限陡峭;相反,你可以在电影播放时放大曲线的陡峭部分,同时以某种方式抵消陡峭化。从这个新的动态视角看,曲线越来越接近一条具有有限陡峭度的冻结曲线。这种变换使得目标——冻结极限——成为一个有限计算机可以处理的有限对象。
巴克马斯特团队意识到,PINN 可能是寻找这些流体方程冻结解的极其高效的方法。此外,这些神经网络还可以确定使奇异解显得冻结和有限的独特缩放率。
起初,他们的 PINN 只发现了已知的候选。例如,在 2022 年,巴克马斯特、布朗大学的哈维尔·戈麦斯 - 塞拉诺及其合作者使用 PINN 逼近了侯和罗在 2013 年发现的稳定爆炸(侯和陈在那年晚些时候证明了其存在)。


特里斯坦·巴克马斯特(左)和哈维尔·戈麦斯 - 塞拉诺正在使用神经网络寻找使流体方程出现故障的极其微妙的方式。
Dan Komoda/ Institute for Advanced Study; Jason Rossi/Brown University
他们还在科尔多瓦 - 科尔多瓦 - 丰特洛斯(CCF)方程中重新发现了一个已知的奇点候选,该方程描述了一种更简单的一维流体。那个奇点候选尤其引人注目——它是不稳定的。它于 2019 年被发现,因为 CCF 方程恰好与一个更简单且被充分理解的流体模型密切相关。但 PINN 能以更通用的方式找到这个解,而且精确得多。这是因为它不是传统意义上的模拟(即让流体随时间逐步前进),而是直接追求冻结极限。
“没有时间,所以你不在乎它是否不稳定,”巴克马斯特说。“你只是试图解方程本身。”
不稳定的新发现与未来展望
巴克马斯特和戈麦斯 - 塞拉诺对使用 PINN 寻找新的不稳定奇点候选感到兴奋。他们与 Google DeepMind 合作,花了几年时间微调神经网络方法,以在几种不同的经典流体理论中寻找不稳定爆炸。现任 DeepMind 研究员的王永吉领导团队从现成的 PINN 转向定制的神经网络,这些网络专门针对他们试图求解的特定流体方程。研究人员还进一步调整了 PINN 的结构,以引导它们找到具有已知奇点应有特征的解。
在此过程中,他们的 PINN 在识别奇点候选方面变得更出色——出色得多。
这些“不稳定的”爆炸几乎不可能被发现,就像大海捞针一样。
今年 9 月,他们由 20 多名研究人员组成的合作团队揭示了许多以前从未见过的奇点,其中大多数是不稳定的。
重新审视罐子中的旋转流体,他们描述了欧拉方程中四个新的不稳定奇点候选。这些仍然与侯和罗已知的稳定奇点大体相似,尽管初始旋转条件在强度和其他变量上略有不同。他们发现的每个候选都比前一个更不稳定——当设置以微妙的方式调整时,消失得更容易。
他们还研究了描述流体如何在二维不可压缩多孔介质(如土壤或岩石)中过滤的方程。在这种设定中,以前从未有人发现过奇点候选。他们发现了四个——一个稳定,三个不稳定。所有这些都涉及一个可以在思想实验中可视化的类似设置,尽管现实中,没有科学家能够以实验成为现实所需的无限精度来调整流体。想象一个充满沙层和岩石层的蚂蚁农场(但没有蚂蚁)。现在加入一滴水,湿润一些沙子。随着时间的推移,重力将水拉下穿过沙子,水滴在下落过程中变平。最终,它撞击到岩石层,与流体密度相关的某个属性似乎会爆炸。
最后,该团队回到了一维 CCF 方程,这次发现了一个比以前更不稳定的奇点。可视化这个模型的一种方式是想象一个广阔的水坑,其中有两股相反的洋流。CCF 方程描述了两股洋流之间的界面。如果你在这个界面中放入一个精心设计的扭结,它会锐化成一个奇异的尖点。
值得注意的是,与纳维 - 斯托克斯方程一样(并且与研究人员研究的其他两种方程不同),CCF 方程描述的流体具有类似于粘性的耗散特性。因此,他们研究的每个模型都表明,PINN 方法可以处理完整纳维 - 斯托克斯方程的某些具有挑战性的方面,例如更高的维度和耗散。
“我们试图逐一隔离技术难点,”戈麦斯 - 塞拉诺说。
至关重要的是,这些新的奇点候选都尚未被证明。但戈麦斯 - 塞拉诺预计它们可以被证明,因为 PINN 的近似非常精确。候选越精确,就越容易证明它是一个真正的奇点。与几年前团队首次使用 PINN 时相比,他们的精度提高了大约十亿倍。
“精度非常出色,”西班牙加泰罗尼亚理工大学数学家伊娃·米兰达说。“残差误差如此之小,以至于这些解确实可以用作未来计算机辅助证明的种子。”
逃离边界的竞赛与百万美元挑战

Google Deepmind 的研究员王永吉开发了许多技术创新,使得发现新的不稳定奇点候选成为可能。
Sang He
百万美元的问题——或者从技术上讲,是百万美元问题的热身问题——在于 DeepMind 合作团队现在是否可以使用他们的 PINN 机制在欧拉方程中找到奇点:针对一个没有被困在罐子里的流体。这是一个困难得多的问题。数学家们表示,他们需要再次升级技术来处理这种更狂野、更复杂的流体,但他们持乐观态度。
“你正在构建一个强大的工具来寻找非常难以找到的东西,”巴克马斯特说。
然而,其他数学家指出,过去的成功并不能保证未来的回报,因为无界流体与有界流体完全不同。“这是完全不同的动物,”西班牙数学科学研究所数学家迭戈·科尔多瓦说,他是 CCF 模型中的科尔多瓦之一(他的父亲是另一位)。
因此,随着研究人员在欧拉方程及其他方程中寻找“无边界”奇点,竞争正在升温。科尔多瓦和他的合作者、西班牙 CUNEF 大学的路易斯·马丁内斯 - 索罗亚已经使用纸笔技术在一系列不同的流体设定中发现了稳定奇点。他们相信他们的方法即将适用于无边界欧拉流体(科尔多瓦曾担心 DeepMind 合作团队会先于他们达到这个目标,但令他欣慰的是,他们的 PINN 还不够强大来解决这个问题。他说,他们找到的解“是不稳定的,但没那么不稳定”)。
另一位竞争者、加州大学圣地亚哥分校的塔雷克·埃尔金迪已经在无边界设定中取得了成功(尽管有其他注意事项),并且也打算扩展他的策略范围。
目前尚不清楚哪种技术(如果有的话)会到达终点线。“如果哈维能做到,我会非常自豪和高兴,”科尔多瓦说(他是戈麦斯 - 塞拉诺的博士生导师)。“但如果我们能做到,我会更高兴。”
如果有人能做到,那么接下来就是纳维 - 斯托克斯方程。但尽管最近在寻找新的流体缺陷方面取得了一系列进展,数学家们仍不敢抱太高的期望。
“你可以做白日梦,但只能做一两天,”戈麦斯 - 塞拉诺说。“你没有足够好的想法。然后白日梦就停止了。”


